研究活動紹介
算数・数学を理解するための学習方法 ―関数概念の獲得―
| 名前 | 二澤 善紀(教育学部 教育学科) |
|---|---|
| 科研費種別 | 基盤研究C |
| 研究課題 | 学習者の関数理解の様相分析に基づく事象を数理的に捉える力の育成に関わる研究 |
| 研究期間 | 2017 〜2019 |
研究目的
研究背景
小学校・中学校の算数・数学教育における関数学習に課題があることは、以前より指摘されている。また、現在の小中学校における関数学習は、幼児の頃から形成が始まっているとされる2変量の関係付け(Fig.1)が十分に生かされているとはいえない可能性がある。従って、児童生徒の認知・認識を考慮した学習のあり方の検討が必要である。

Fig.1 幼児の頃から形成が始まっている時間と道のり(2変量)の関係付け
研究対象
関数学習において、次の内容を学習する段階を対象とする。
(Ⅰ)事象の変化を量的に捉えて変量を抽出する。
(Ⅱ)抽出した変量から関数関係を見いだし対応させる。
研究目的
- 児童生徒の認知・認識を考慮して関数学習を進めていく上での学習モデルを構築すること。
- 構築した学習モデルに基づき、事象を数理的に捉える力を育成する学習のあり方を示すこと。
研究方法
- 児童生徒の数学概念の認知に関する先行研究を整理・分析する。
- 数学概念の認知に関する先行研究の整理・分析を基礎にして、関数の学習に関する学習モデルの構築を図る。
- 構築した関数の学習モデルに基づき関数学習の先行研究を分析し、関数理解のための途上概念を焦点化する、また焦点化した途上概念を形成するための教材開発に取り組む。
- 開発した教材の有効性について、教育実践を通して検証する。
研究成果
- 児童生徒の数学概念の認知に関する先行研究から、数学を理解する、あるいは数学概念を形成するためには、その基になる概念が児童生徒に形成されていることが必要であることを示すことができた。
-
認知に関する先行研究の分析を基礎にして、児童生徒の認知・認識を考慮した関数の学習モデルを構築した(Fig.2)。
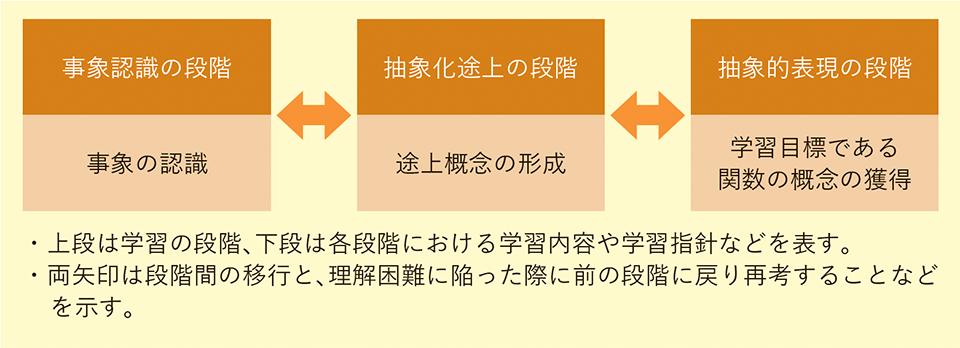
Fig.2 関数の学習モデル
- 関数の学習モデルに基づき、関数理解のための途上概念は「一方が増えると他方が増える」、「一方が増えると他方は減る」というような論理構造をもつ質的な関係概念で、「論理構造をもつ質的な(Ⅰ)と(Ⅱ)に関する途上概念」と焦点化できた。さらに、現在の関数学習は数値や文字を用いる学習が主であるが、児童生徒の関数学習を「数値を用いない学習」と「数値や文字を用いる学習」に大別した(Fig.3)。数値を用いない学習は、これまでの関数学習には見られなかった新たな学習段階であり、この段階で焦点化した途上概念を形成できることを理論的に示すことができた。
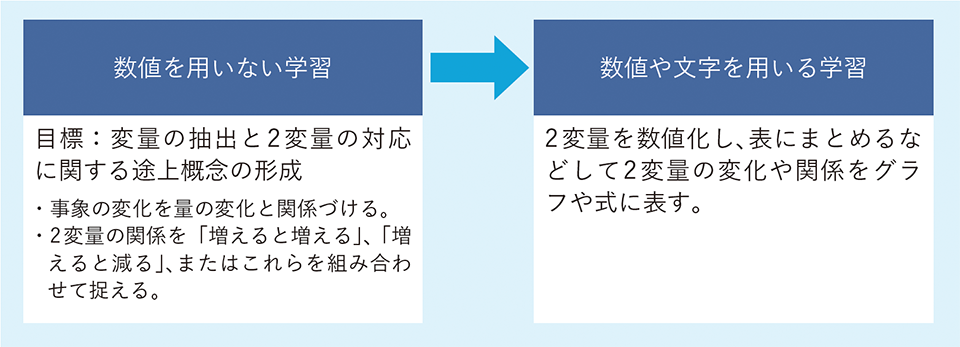
Fig.3(Ⅰ)と(Ⅱ)に関する途上概念の形成のための学習の枠組み
-
焦点化した途上概念を形成するために、時間を主軸にする教材を開発し(Fig.4)、小学校第4学年の児童を対象に有効性を検証した。その結果、焦点化した途上概念は、開発した時間を主軸にする教材を用いて「数値を用いない学習」で形成できること、関数理解の促進には、数値を用いない学習が有効であることを得た。

Fig.4 時間を主軸にする教材:時間が介在する2変量の関係(左)、円錐状の立体の影の様子(中)と記録例(右)
研究者紹介

二澤 善紀(教育学部 教育学科)
専門分野
数学教育学
科学研究費採択
- 基盤研究C「創造性育成のための数学の体系的理解を取り入れた数学的モデリング教材と授業の研究」2014-2016
最近の業績
- 算数・数学における関数概念の認識発達を培う理論と実践(2020年)
- 関数の学習指導における課題と展望(数学教育学会・2019年)
- 小学校段階における関数学習の基礎研究(数学教育学会・2019年)
- 関数指導における教材開発のための基礎的研究-関数指導の体系に着目して(数学教育学・2018年)
- Applying van Hiele’s Levels to Basic Research on the Difficulty Factors behind Understanding Functions(International Electronic Journal of Mathematics Education・2018)
その他業績

出版物
算数・数学における関数概念の認識発達を培う理論と実践
(ミネルヴァ書房)
2020年









